Playing Atari with Deep Reinforcement Learning

Basic Information

• 2013 NeurIPS
• Volodymyr Mnih, Koray Kavukcuoglu David Silver et al.
• 這個論文提出的做法稱為 DQN(Deep Q-Networks)

問題描述

過去在 RL 領域當中把一些 high-dimensional 的感官資料（如：視覺影像、語音資料等）作為 agent 的輸入去學習一直是一個很大的挑戰。然而我們也看到近幾年 Deep Learning 已經能夠在這種資料上去擷取特徵，進而去完成許多複雜的任務。

所以「能不能把 Deep Learning 的成功也放進 RL 當中呢？」這樣的想法自然而然就出現了。

不過從 Deep Learning 的角度來看 RL 的話，會有幾個明顯的問題。

1. RL 的訓練資料（如：Reward）需要透過與環境互動取得，但數值範圍往往很 sparse，而且也往往會經過一段時間的延遲才取得 與 Deep Learning 相較之下，DL 的資料通常都會先 Label 好，可以直接把資料之間的關聯建構起來。
2. RL 的訓練資料具有高度相關性 在 DL 當中我們會預設資料之間是沒有什麼相依性的，但在 RL 當中同一個 episode 的 state、action、reward 之間都會具有相當高的相關性。
3. RL 的資料分佈會隨著 policy 的改變而有巨大幅度的變化 DL 往往假設資料的分布會維持住。

這一篇論文成功將 CNN 應用在 RL 上，也避免了上述提及的幾個問題。

Related Works

• Q-Networks
• TD-gammon
• 收斂性相關研究
  • Residual algorithms: Reinforcement learning with function approximation.
  • Q-learning
• Neural fitted Q-learning (NFQ)

Q-Networks

在 RL 當中我們會透過 MDP 去 model 整個問題，而 RL 的目標就是要讓整體的 reward 總和最大化。

定義 optimal action value function $Q^*$ 如下

$$Q^*(s, a) = \max_{\pi} \mathbb{E} \left[ R_t | s_t = s, a_t = a, \pi \right]$$

也就是在 state $s$ 採取 action $a$ 並 follow policy $\pi$ 得到的最大 return。其中 Return 的定義如下，這裡考慮有 discount 的版本。

$$R_t = \sum_{t' = t}^{T}{\gamma^{t' - t}r_{t'}}$$

• $\gamma$ 為 discount factor
• $r_t$ 表示在時間 $t$ 取得的 reward

既然 RL 的目的是要讓整體的 return 最大化，也就是要找到 $Q^*$ 了。Q-Network 就是用 Neural Network 來近似 $Q^*$，也就是要讓底下的 Loss 最小化。

$$\begin{align*} L_i(\theta_i) &= \mathbb{E}_{s, a \sim \rho(\cdot)}{\left[ \left( y_i - Q(s, a; \theta_i) \right)^2 \right]} \\ y_i &= \mathbb{E}_{s' \sim \varepsilon}{\left[ r + \gamma \max_{a'}{Q(s', a'; \theta_{i-1})} \right]} \end{align*}$$

需要特別注意到對於 $\theta_i$ 來說，他要去近似的是 $\theta_{i-1}$ 的模型得出來的結果，也就是說，Q-Network 透過固定訓練的目標(Target Network)，解決了前面提及的第三個問題「RL 的資料分佈會隨著 policy 的改變而有巨大幅度的變化」。

TD-gammon

一個 model-free RL 算法，透過一個 multi-layer perceptron 和一層 hidden layer 去預測 value function，成功在雙陸棋上面 outperform 人類。

不過這裡的成功只停止在雙陸棋上，並無法繼續擴充到其他的領域。

收斂性相關研究

過去的研究當中發現到如果是 model-free 搭配 non-linear function approximators 或是 off-policy learning 的話會導致 Q-network 發散，無法收斂。

後續的研究中則發現到 Q-network 無法收斂的問題可以透過 gradient TD 舒緩，並且證明了底下兩個狀況是可以確保收斂。

1. 固定 policy，使用非線性的 approximator
2. 使用線性的 approximator 去學 control

然而這些研究都並未能夠給出用非線性去學 control 的方法。

NFQ

跟這一篇 paper 最相近的一個研究，他們會先透過 Computer Vision 的模型萃取出圖片的特徵，然後再把這些特徵丟去給 RL 訓練。

不過 DQN 與 NFQ 不同的地方在於 DQN 是 end-to-end，也就是說可以直接從 visual input 去訓練，而 NFQ 不是。

Methodology

在 TD-gammon 當中我們看到了使用 Neural Network 去學習 value function 有還不錯的成效，DQN 稍微修改了這個做法，將 Q-Network 和 Experience Replay 結合起來。

Experience Replay 會將 agent 跟環境的互動過程當中的 experience 記錄在 replay memory $\mathcal{D}$ 當中。當要去更新模型的時候，我們是從 replay memory 當中取得隨機幾筆去更新。

Info

在時間 $t$ 的 experience 包含了 state, action, reward, next state

$$e_t = (s_t, a_t, r_t, s_{t+1})$$

因此 experience 就定義成

$$\mathcal{D} = e_1, e_2, \dots, e_N$$

在經過 experience replay 之後，agent 會透過 $\epsilon$-greedy 去選擇 action。

實作上 experience 只會儲存最後 $N$ 筆，並且 history 當中的 frames 只會取出最後 4 個，拿出來做一些 preprocess $\phi(s)$ 之後作為實際上儲存進 experience 的 state。

image

Image from Volodymyr Mnih, Koray Kavukcuoglu, David Silver et al. (2015)

透過 Q-Network 中的 Target Network 以及 Experience Replay，DQN 順利避免了最初提及的兩個問題「RL 的訓練資料具有高度相關性」以及「RL 的資料分佈會隨著 policy 的改變而有巨大幅度的變化」。

Results

實驗設定

實驗做在 7 個 Atari games，Beam Rider, Breakout, Enduro, Pong, Q*bert, Seaquest 以及 Space Invaders。

每個遊戲的 reward 一開始都不太相同，實驗上調整了 reward 的大小，使得所有 positive reward 固定為 $1$；negative reward 為 $-1$，其餘則為 $0$ 表示不影響。

並且會使用 frame skipping 的技巧，讓 agent 只會每經過 $k$ 個 frames 才會去擷取畫面，並且做出相對應的 action。至於那些被忽略的 frames，就持續上一個做出的 action。除了 Space Invaders 因為遊戲當中的雷射會跑很快，所以設定 $k = 3$，其他遊戲則都是 $k = 4$。

評估方式

在 Deep Learning 當中如果要評估一個 Network 的好壞，可以單純透過觀察模型在 validation set 上的 performance 即可，但是在 RL 當中並沒有 validation set，因此評估一個 agent 的好壞就相對困難。

過去會透過多次遊戲中 agent 獲得的 reward 平均去評估，也就是說理想上每經過一輪更新，模型能夠得到的 reward 應該要慢慢變大。不過作者發現在他們的模型得出來的結果往往會是很不穩定的。作者推測是因為權重即便只有小的變化也會對 policy distribution 有大的影響，導致接下來會經過的 state 就很不相同。

因此作者改成 Q 的平均去評估，也確實發現會平滑許多。

image

Image from Volodymyr Mnih, Koray Kavukcuoglu, David Silver et al. (2015)

比較基準

最後將 DQN 跟幾個 Baseline 去比較

• Sarsa
  • On-control policy
  • Linear approximator
  • 人工提取 features
• Contingency
  • 跟 Sarsa 類似，但有包含了部分的學習過程
• HNeat Best
  • 訓練的過程包含了一點專家系統的概念
  • 事先標記好 object 的位置以及類型
• HNeat Pixel
  • 訓練的過程包含了一點專家系統的概念
  • 事先處理好了 8 color channel representation
• Human

image

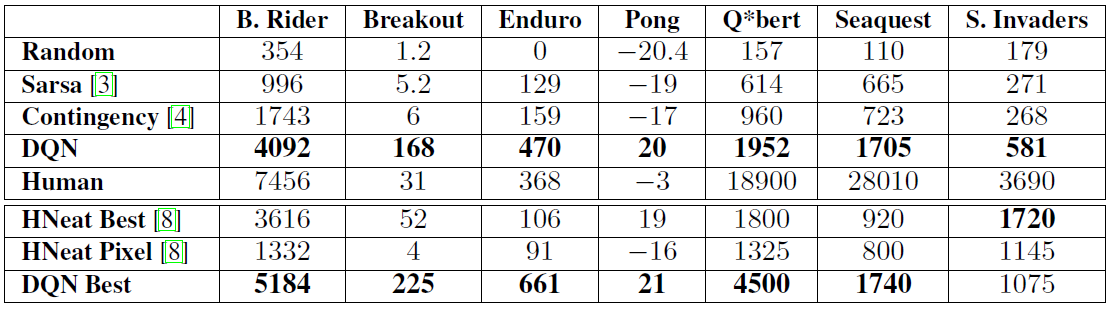
Image from Volodymyr Mnih, Koray Kavukcuoglu, David Silver et al. (2015)

最後得出來的結果，DQN 在幾乎所有的遊戲當中都 outperform 所有的算法，證明了 DQN 的成功。

Contribution

• 成功結合 Deep Learning 以及 Reinforcement Learning
• 直接從 raw RGB 當作輸入，不需要事先經過其他的分解
• 透過 Experience Replay 以及 Target Network 解決過去 Deep Learning 結合 RL 時訓練不佳的問題