Agent57: Outperforming the Atari Human Benchmark

Basic Information

• Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski, et al. @ Google DeepMind
• 2020 ICML

問題描述

在 RL 當中，Atari games 是一個相當重要的 benchmark。過去的 RL 模型已經能夠在大多的 atari games 當中獲得相當不錯的 performance，例如 MuZero、R2D2，分別在 57 個遊戲當中有 51 和 52 個遊戲是 outperform 人類的。不過可惜的是，在剩下的遊戲當中這些 SoTA 就通常完全沒辦法學習。

Info

稍微翻了一下 MuZero 以及 R2D2 兩篇 paper 的結果，分別是這些遊戲 performance 不太好。

• MuZero
  • montezuma revenge, pitfall, private eye, skiing, solaris, venture
• R2D2
  • montezuma revenge, pitfall, private eye, skiing, solaris

那麼，剩下這些遊戲有怎樣的共通點呢？

skiing 和 solaris 這兩款遊戲中我們發現到他們都需要相當長的時間之後才會得到 reward，在遊戲的過程當中並不會馬上知道現在這個操作對未來會有正面或是負面的影響。

Skiing game on Atari 2600. Video from TheLimeyDragon

以 Skiing 這款遊戲來說，玩家要操作角色滑雪，途中要盡可能快速通過指定數量的 gates。每忽略一個 gate 就會多 5 秒的 penalty。Reward 會一直到遊戲的最後依照最後通過的時間決定。

剩下的四款遊戲則是因為環境太大，又有不少的 negative reward，需要相當大量的探索之後才能得到 positive reward。

Pitfall game on Atari 2600. Video from The No Swear Gamer

以 Ptifall 這款遊戲來說，玩家要操作主角在 20 分鐘的時間探索 255 個遊戲場景，去找到藏在地圖當中的寶藏。過程中有許多陷阱，找到寶藏可以加分，最後分數越多越好。

從這些觀察當中可以得到兩個待改善的地方

1. long-term credit assignment 如何決定哪些 action 應該要給 positive 或是 negative reward
2. exploration 如何讓 agent 能夠盡可能去正確探索環境

   之所以說"正確"，是因為即便是在很多 negative reward 的地方，也需要嘗試越過那些障礙，也許才有機會遇到 positive reward。

這一篇 paper 希望改善這兩個對 RL 相當重要的問題，也提出了一個可以在所有 57 Atari games 都 outperform 人類的 RL 模型。

Related Works

Never Give Up

Never Give Up(NGU) 目的也是希望能夠讓 RL agent 能夠在上述 hard-exploration 的環境當中有更好的成效。具體來說 NGU 包含了幾個重要的部分。

• Intrinsic Reward
• UVFA
• RL Loss
• NGU Agent

Intrinsic Reward

在 Intrinsic Reward 的部分目的也是希望能夠促使 agent 多多探索，他們將 reward 分成了兩個部分，分別是 per-episode novelty $r_{t}^{\texttt{episodic}}$ 以及 life-long novelty $\alpha_t$。這兩者分別會讓 agent 鼓勵去探索那些在 episode 當中、在整個訓練過程當中沒有踏足過的狀態。而整體 intrinsic Reward 如下。

$$r_t^i = r_{t}^{\texttt{episodic}} \cdot \min \{ \max \{ \alpha_t, 1 \}, L \} \quad (L = 5)$$

$\min$ 和 $\max$ 只是用來限制 life-long novelty 的範圍，避免太大或是太小。

Image from Adrià Puigdomènech Badia, Pablo Sprechmann et al. (2020)

而整體的 reward 依照過去 curiosity-driven exploration 的研究，設定如下。

$$r_t^{\beta_i} = r_t^e + \beta_ir_t^i$$

• $r_t^e$ 是 Extrinsic Reward，在 RL 當中就是環境給予的 reward
• $r_t^i$ 是 Intrinsic Reward，也就是前面定義的 reward
• $\beta_i$ 用來調整兩種 reward 的影響程度

不同的環境下需要的 exploration 以及 exploitation 是不同的。當 $\beta$ 比較大的時候，intrinsic reward 會使得 agent 比較傾向去試試看那些不熟的 state，反之則會去走那些比較熟悉的。

UVFA

NGU 接下來用 Universal Value Function Approximator, UVFA 去近似 action value function $Q$。

$$Q(s_t, a_t, \beta_i) = \mathbb{E} \left[ r_{t+1}^{\beta_i} + \gamma_i r_{t+2}^{\beta_i} + \gamma^2r_{t+3}^{\beta_i} + \dots | s_t, a_t, \beta_i \right]$$

針對不同的 $\beta_i$，NGU 會選擇不同的 $\gamma$。

• $\beta_i$ 大，傾向 exploration，不需要看太遠，$\gamma$ 選小一些
• $\beta_i$ 小，傾向 exploitation，需要看遠一些，$\gamma$ 選大一些

Image from Adrià Puigdomènech Badia, Pablo Sprechmann et al. (2020)

左邊是 $\beta$ 選擇的分布，右邊是 $\gamma$ 的分布。

RL Loss

既然有 NN 去逼近，那也就會有 Loss。NGU 計算 Loss 的方式是採用 Transformed Retrace Double Q-learning Loss。

Retrace 是一個可以用來評估或是用在 control 上的 RL 演算法。在這邊我們在意的是評估的部分，Retrace 可以幫助我們去評估如果我們 follow policy $\mu$，在目標的 policy $\pi$ 的 action value function $Q^\pi$ 可以拿到多少 Reward。

首先定義從 policy $\mu$ 當中取得的 trajectories $\tau$

$$\tau = (x_t, a_t, r_t, x_{t+1})_{t \in \mathbb{N}}$$

考慮有限的 sampled sequences，定義 Retrace operator

$$\hat{T}Q(x_t, a_t) = Q(x_t, a_t) + \sum_{s = t}^{t + k - 1}{\gamma^{s - t} \left( \prod_{i = t+1}^{s}{c_i} \right) \delta_s}$$

其中

$$\begin{align*} \delta_t &= r_t + \gamma \sum_{a \in \mathcal{A}}{\pi(a | x_{t+1})Q(x_{t+1}, a) - Q(x_t, a_t)} \\ c_s &= \lambda \min \left( 1, \frac{\pi(a_s | x_s)}{\mu(a_s|x_s)} \right) \end{align*}$$

實際上訓練的 NN 會有兩個，就跟 DQN 一樣，一個是 target network，一個是 online network。Target network 就可以透過 Retrace operation 去得到目標 $\hat{y_t}$

$$\hat{y_t} = \hat{T}Q(x_t, a_t; \theta^-)$$

$\theta^-$ 是 target network 的 parameter。

有了目標，也就能夠得到 Loss

$$L(x_t, a_t, \theta) = \left( Q(x_t, a_t, \theta) - \hat{y_t} \right)^2$$

Tips

上面提及的是單純的 Retrace Double Q-learning Loss，實際上還會為了讓 NN 更好學習，改成 Transformed 版本。

$$\mathcal{T}^hQ(x, a) = \mathbb{E}_{\mu} \left[ h \left( h^{-1}(Q(x, a)) + \sum_{t \geq 0}{\gamma^t \left( \prod_{s=1}^t{c_s} \right) \delta_t^h} \right) \right]$$

其中

$$\delta_t^h = r_t + \gamma \sum_{a \in \mathcal{A}}{\pi(a | x_{t+1})h^{-1}(Q(x_{t+1}, a) - h^{-1}Q(x_t, a_t))}$$

$$\begin{align*} \forall z \in \mathbb{R}, h(z) &= \texttt{sgn}(z)\left(\sqrt{|z| + 1} - 1\right) + \epsilon z \\ \forall z \in \mathbb{R}, h^{-1}(z) &= \texttt{sgn}(z)\left(\left( \frac{\sqrt{1 + 4\epsilon(|z| + 1 + \epsilon)} - 1}{2\epsilon} \right) - 1\right) \end{align*}$$

但數學有點太難，我還沒有理解這一段做了什麼。

NGU Agent

NGU 基本上使用了 R2D2，只不過輸入上會丟

• Action $a_{t-1}$
• Extrinsic Reward $r_{t-1}^e$
• Intrinsic Reward $r_{t-1}^i$
• $\beta_i$

Image from Adrià Puigdomènech Badia, Pablo Sprechmann et al. (2020)

NGU 採用分散式學習，有許多的 actor 使用不同的 $\beta_i$ 取得不同的 experience 丟在 replay buffer，然後再讓 learner 使用 experience 去更新參數學習。

最後只需要設定 $\beta = 0$，就可以得到單純 exploitation 的模型當成最後的結果。

NGU 的問題

1. 實作上 NGU 有時會很不穩定、難以收斂，尤其當 $r_t^i$ 和 $r_t^e$ 的大小、分布相當不同時
   • Agent57 的作者認為是因為 NGU 只用了一個 NN 去學習導致
2. 不是那麼地 general
   • 解決了一些 hard-exploration 的問題，卻在一些簡單的問題做得很差

     Image from Adrià Puigdomènech Badia, Pablo Sprechmann et al. (2020)

3. 每種 policy(不同 $\beta_i$ 的選擇) sample 的 experience 數量相同
   • 有些 policy 對於學習是並沒有幫助的，但是卻跟其他人有同樣的影響力
   • 有些環境需要更多的 exploration，有些則不需要
4. 無法好好處理 long-term credit assignment 問題
   • 例如在 skiiing 以及 solaris 就做得頗差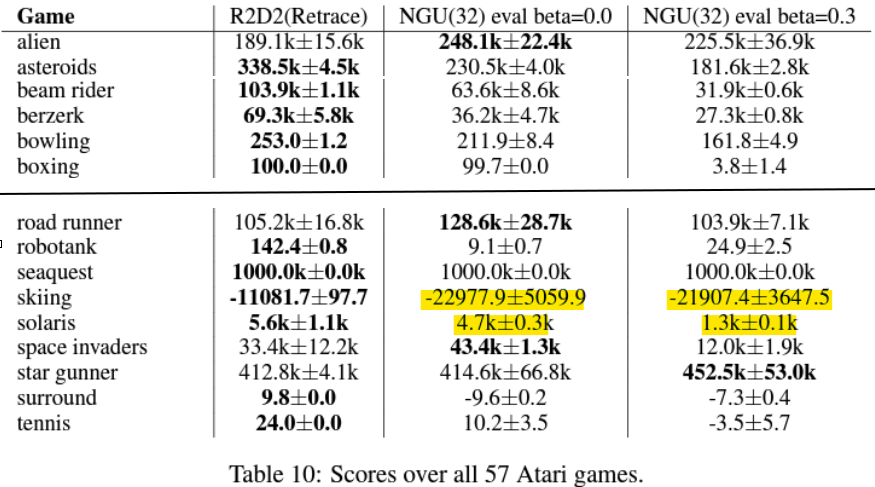

     Image from Adrià Puigdomènech Badia, Pablo Sprechmann et al. (2020)

Methodology

State-Action Value Function Parameterization

Agent57 首先針對 State-Action Value Function 拆開來，用兩個 NN 分別去針對 Extrinsic 以及 Intrinsic Reward 處理。

$$Q(x, a, j; \theta) = Q(x, a, j; \theta^e) + \beta_j Q(x, a, j; \theta^i)$$

• $x$: state
• $a$: action
• $j$: 表示使用的是哪一個 policy 的 one-hot vector
• $\theta^e$: 近似 Extrinsic Reward $r^e$ 的 NN
• $\theta^i$: 近似 Intrinsic Reward $r^i$ 的 NN
• $\theta$: $\theta^e \cup \theta^i$

兩個 Q-Network 都會接收同樣的 state 和 action，並且也是 follow 相同的 policy $\pi$。

$$\pi(x) = \arg \max_{a \in \mathcal{A}}{Q(x, a, j; \theta)}$$

兩個模型都是使用 Transformed Retrace Loss，跟 NGU 是一樣的，不過在計算 Loss 時 reward 的部分是分別給 $r^e$ 和 $r^i$。

細節上，因為是一次更新 $B$ 個 batch，每個 batch sample 的 sequence 大小為 $H$，因此 Loss 會有兩組總和。

$$L(D, \theta, \theta^-, \pi, \mu, r, h) = \sum_{b = 0}^{B-1} \sum_{s=t}^{t+H-1}{\left( Q(x_s^b, a_s^b; \theta) - \hat{T}_{r, h}^{\mu, \pi}Q(x_s^b, a_s^b; \theta^-) \right)^2}$$

• $D$ 表示從 $\mu$ sample 出來的 trajectories
• $\theta$ 為 online network 的參數
• $\theta^-$ 為 target network 的參數
• $\pi$ 為目標 policy
• $\mu$ 為當前 policy
• $r$ 表示 reward，上面的差異就是這裡傳入的分別是 $r^e$ 和 $r^i$
• $h$ 為 Transformed Retrace Operator 的 $h$
• $x_s^b$ 是在 batch $b$、時間 $s$ 的 state
• $a_s^b$ 是在 batch $b$、時間 $s$ 的 action

於是 Agent57 的模型變成底下的樣子。

Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

Note: 雖然兩個模型都會把 intrinsic 以及 extrinsic reward 輸入進去，但 Loss 在計算上分別都只會拿自己的。

---

Tips

作者也在論文當中證明了這種拆開來訓練的方法是等價於沒有拆開來訓練的樣子，也就是說這種做法的正確性是被確保的(無論是否有使用 Transformed 的版本)。

不過實際上訓練時因為拆開來訓練，能夠使模型更好去學習各自的 reward，以達到更好的訓練成效。

透過拆開訓練，解決了 NGU 不穩定、難以收斂的問題。

---

Adaptive Exploration over a Family of Policies (Bandit)

「每種 policy sample 的 experience 數量相同」這個問題 Agent57 透過加上 Meta-controller 來解決。

Tips

如果每個 actor 都能夠學習什麼時候該 exploit、什麼時候該 explore，選擇出現傾向，不同 policy 就有不同重要程度了

舉一個例子來說，NGU 會把每個 actor 都當成是工廠生產出來的機器人，每一個 actor 一開始都是一樣的。

接下來依照你的需求不同，你分別把這幾個 actor 加上不同的偏好，有些傾向 exploration，有些傾向 exploitation。

這些 actor 就會去環境當中互動，蒐集一些 experience 給你學習。

另一方面，Agent57 的 actor 天生就有一些自己的偏好，有人天生愛探險，有人天生愛保險。

但是他們在跟環境互動的過程當中會慢慢發現到自己的性格怎樣調整會在這個環境當中獲得更好的 reward。

最後你一樣可以透過這些 actor 蒐集的 experience 去學習。但是 policy 不會被固定下來，具有更高的靈活性。

照著這樣的想法，Agent57 讓每個 actor 前面都加上一組 Meta-controller，在每一個 episode 開始之前，透過它決定接下來要使用的 $(\beta_j, \gamma_j)$。此外，Meta-controller 也會依據得到的 reward 去調整選擇不同 $j$ 的機率。

如此一來，每個 actor 就會因為 Meta-controller 的存在，產生出選擇 policy 的傾向，進而使得整體訓練採用的 experience 中 policy 的比例改變。

Warning

細節上，每個 actor 選擇 action 都是採用 $\epsilon_l$-greedy，其中的 $l$ 表示不同的 actor。亦即，不同 actor 採用不同的 $\epsilon$ 大小，也因為如此，Meta-controller 是每個 actor 各有一個。

Upper Confidence Bound Algorithm (UCB)

Agent57 把 Meta-controller 簡單設計成一個 Multi-Arm Bandit (MAB) 問題，也就是說我現在面前有 $N$ 個 action $\{0, \dots, N-1\}$ 可以選擇，在時間 $k$ 你選擇 $A_k$，目標是在整個 horizon $K$ 當中你可以得到最好的 return，也就是讓底下的期望值最大化。

$$\mathbb{E}_{\pi}{\left[ \sum_{k=0}^{K-1}{R_{k}(A_k)} \right]}$$

過去對於 MAB 在 reward 的分布是固定的狀況下會使用 UCB 來解決它。基本的想法是對每個不同的選擇去評估每個決策的信賴區間的上界，把這個上界當成是它預期的 return，選擇其中最大的當成這次的選擇。

• 未知/嘗試次數少的選擇 (不確定性高，要傾向 exploration)
  • 平均 Return 低 ➡️ UCB 高 ➡️ 探索機率高
  • 平均 Return 高 ➡️ UCB 更高 ➡️ 探索機率更高
• 已知/嘗試次數多的選擇 (不確定性低，要傾向 exploitation)
  • 平均 Return 低 ➡️ UCB 低 ➡️ 嘗試機率低
  • 平均 Return 高 ➡️ UCB 高 ➡️ 嘗試機率高

$$A_k = \begin{cases} k & \forall 0 \leq k \leq N-1 \\ \arg \max_{1 \leq a \leq N}{\hat{\mu}_{k-1}(a) + \beta \sqrt{\frac{\log(k-1)}{N_{k-1}(a)}}} & \forall N \leq k \leq K-1 \end{cases}$$

其中

$$\begin{align*} N_{k}(a) &= \sum_{m=0}^{k-1}{\mathbb{1}_{\{A_m = a\}}} \\ \hat{\mu}_{k}(a) &= \frac{1}{N_k(a)} \sum_{m=0}^{k-1}{R_k(a) \mathbb{1}_{\{A_m = a\}}} \end{align*}$$

也就是說

• $N_k(a)$ 用來表示一個 action $a$ 至今被嘗試的次數
• $\hat{\mu}_k(a)$ 用來表示一個 action $a$ 至今平均的 Return

從式子當中也可以觀察到，確實它會傾向讓 平均 Return 高 或是 嘗試次數少 的選項有更高機率被選擇到。

Sliding-Window UCB

然而，如果 reward 的分布會變動的話，單純的 UCB 並不會是一個好的選項，因為過去的經驗即便在現實狀況改變仍然有大影響力。而隨著 agent 更新、行為模式改變，reward 的分布也會變動。

這裡的經驗指的是一個 action 採取的次數以及得到的 Return 平均 ($N_k(a)$ 和 $\hat{\mu}_k(a)$)。

因此 Sliding-Window UCB 加上了一個 window length $\tau \in \mathbb{N}^*$ 來限制要考慮多久之前的經驗。

$\tau$ 的選擇應遠比 $K$ 小。

$$A_k = \begin{cases} k & \forall 0 \leq k \leq N-1 \\ \arg \max_{1 \leq a \leq N}{\hat{\mu}_{k-1}(a, \textcolor{red}{\tau}) + \beta \sqrt{\frac{\log(\textcolor{red}{\min(k-1, \tau)})}{N_{k-1}(a, \textcolor{red}{\tau})}}} & \forall N \leq k \leq K-1 \end{cases}$$

其中

$$\begin{align*} N_{k}(a, \textcolor{red}{\tau}) &= \sum_{m=\textcolor{red}{\max(0, k-\tau)}}^{k-1}{\mathbb{1}_{\{A_m = a\}}} \\ \hat{\mu}_k(a, \textcolor{red}{\tau}) &= \frac{1}{N_k(a, \textcolor{red}{\tau})} \sum_{m = \textcolor{red}{\max(0, k-\tau)}}^{k-1}{R_k(a) \mathbb{1}_{\{A_m = a\}}} \end{align*}$$

僅僅是加上 $\tau$ 而已，剩餘的都是相同的。

Simplified Sliding-Window UCB

最後，Agent57 對 Sliding-Window UCB 做了兩個小修正

1. $\log$ 對於結果並不會有影響，可以移除
2. 多加上 $\epsilon$-greedy

$$A_k = \begin{cases} k & \forall 0 \leq k \leq N-1 \\ \arg \max_{1 \leq a \leq N}{\hat{\mu}_{k-1}(a, \tau) + \beta \sqrt{\frac{\textcolor{red}{1}}{N_{k-1}(a, \tau)}}} & \forall N \leq k \leq K-1, \textcolor{red}{U_k \geq \epsilon_{\texttt{UCB}}} \\ \textcolor{red}{Y_k} & \forall N \leq k \leq K-1, \textcolor{red}{U_k < \epsilon_{\texttt{UCB}}} \end{cases}$$

其中

• $\epsilon_{\texttt{UCB}}$ 是一個 hyperparameter
• $U_k$ 是一個 $[0, 1]$ 之間均勻分布的隨機值
• $Y_k$ 是一個 $\{0, \dots, N-1\}$ 之間均勻分布的隨機 action

---

Tips

透過 Bandit，每個 actor 能夠調整自己的 $(\gamma, \beta)$，解決了 NGU「不是那麼地 general」、「每種 policy sample 的 experience 數量相同」這兩個問題。

---

Backprop Through Time Window Size

原先 R2D2 在 Replay buffer 的設計是採用 trace length 80 搭配 replay period 40，作者在實驗當中發現如果採用 trace length 160 搭配 replay period 80，也就是 long trace 的話，對於 long-term credit assignment 的問題似乎能夠得到改善。

---

Tips

透過 long trace 解決了 NGU「無法好好處理 long-term credit assignment」的問題。

---

High-level architecture

Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

Actors

1. 每個 episode 開始前，透過各自的 Meta-Controller 選擇出一組 $(\gamma_j, \beta_j)$
2. 透過上一個 trajectory $(x_t, r_{t-1}^e, r_{t-1}^i, a_{t-1}, h_{t-1})$ 估計當前 state-action value $Q(x_t, \cdot, j, \theta_l)$
3. 透過 $\epsilon_l$-greedy 選擇 action
4. 計算 intrinsic reward $r_t^i$
5. 環境中取得 observation $x_{t+1}$, extrinsic reward $r_t^e$
6. 若已經又經過 400 個 frames，更新模型參數
7. 重複 2 直到 episode 結束
8. 將 trajectories 交給 replay buffer

$\epsilon_l$ 的選擇根據 Dan Horgan, John Quan, David Budden, et al. (2018) 如下

$$\epsilon_l = \epsilon^{1 + \alpha\frac{1}{L - 1}}$$

其他部分基本上都跟 NGU 相同。總之，Actors 去跟環境互動，取得 experience 之後交給 replay buffer，Learner 會從 replay buffer 當中 sample 一些 experience 學習，然後繼續跟環境互動。

Results

Settings

Agent57 在 $\gamma$ 的分布上有做了一點調整，範圍變成 $[0.99, 0.9999]$，具體來說如下圖

image

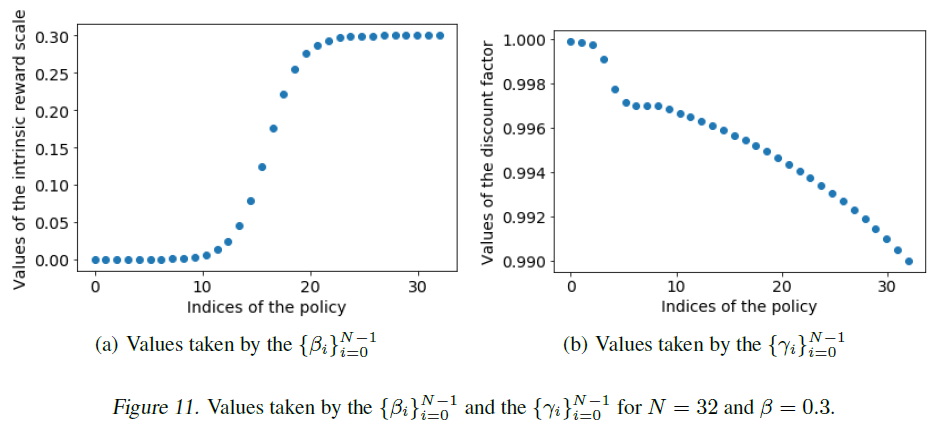
Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

其他 Hyperparameter 的設定詳閱論文的 Appendix G，這裡就不贅述。

對於每個實驗的 Agent 都另外加上一個 Evaluator 去紀錄訓練過程當中的 undiscounted episode returns。

此外，他們並不是採用 Human Normalized Scores (HNS)，而是 Capped Human Normalized Scores (CHNS)，這個測量標準比較強調那些 HNS 比較差的結果，也限制了數值範圍，因此會比較能夠好好評估 general performance。

$$\texttt{CHNS} = \max\{ \min \{ \texttt{HNS}, 1 \}, 0 \}$$

其中

$$\texttt{HNS} = \frac{\texttt{Agent}_{score} - \texttt{Random}_{score}}{\texttt{Human}_{score} - \texttt{Random}_{score}}$$

State-Action Value Function Parameterization

我們透過 intrinsic 以及 extrinsic 拆開來解決 NGU 的缺陷，這裡要來實驗這一個做法實際上帶來多少影響。

作者建構一個簡單的 $15 \times 15$ Gridworld random coin。在每個 episode 開始之前他們把一個 agent 以及一個 coin 隨機地放在地圖上的任意格子。Agent 能夠上、下、左、右移動，並且每個 episode 最多 200 個 steps。當 Agent 走到 coin 會得到 reward 1，然後結束這個 episode。

接著作者比較 NGU 以及 NGU 加上 separate network 的做法。如同前面提及 $\beta_j$ 如果選擇較大，由於 intrinsic reward 有較大的影響，agent 會偏向 exploration，反之則是 exploitation。細節上，$\beta_j$ 的設定會透過 $\beta$ 來調整整體 $\beta_j$ 的大小。

image

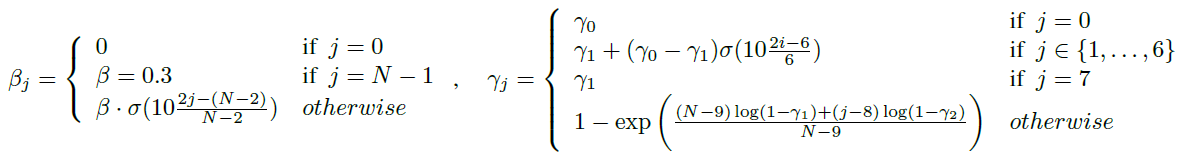
Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

作者比較兩個模型在不同 $\beta$ 的大小下，各自最傾向 exploration ($\beta_j = \max_j \beta_j$) 以及最傾向 exploitation ($\beta_j = 0$) 的設定取得的 Extrinsic Reward。

Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

• $x$ 軸表示 $\beta$ (注意並不是 $\beta_j$)
• $y$ 軸表示 extrinsic reward
• 紫色圓點表示 $\beta_j = 0$，最傾向 exploitation 的狀況
• 綠色圓點表示 $\beta_j = \max_j \beta_j$，最傾向 exploration 的狀況

從結果可以發現到 NGU 在不同 $\beta$ 的設定下會大程度影響到最終 exploitation 的結果，即便這個環境設定是相當簡單的，最終 Return 的趨勢仍然是隨著 $\beta$ 越大變得越小。

另一方面，加上了 separate network 的狀況下 exploitation 的 return 基本上都相當接近 $1.0$，也就是說能夠順利到達 coin 所在的位置。

在 exploration 的部分也可以發現到兩者的發展方向會稍有不同。但整體來說兩者都能在最後趨近於 $0.0$。

由此可見，當 $\beta$ 提升，由於 intrinsic reward 與 extrinsic reward 的大小相差越來越懸殊，導致 NGU 並無法好好只透過一個 NN 去學習，進而影響到結果，較不具有彈性。相對的，增加 separate network 確實能夠帶來相當好的效益。

此外，作者也發現如果把 Agent57 的 separate network 移除，performance 會掉 20% 以上，可見 separate network 的重要性。

作者也發現到 separate network 在最傾向 exploration 的模型會盡可能避開 coin，反之會走出最短路。

Tips

值得一提的是，這個結果如果在取得 coin 之後仍然不會停止的話就不會出現。

Backprop Through Time Window Size

在 trace length 以及對應的 replay period 有多少影響呢？

作者將 R2D2 以及 Agent57 分別用 small trace 以及 long trace 來比較，作者認為在這兩者都有一個共通點：Long trace 會導致訓練前期較為緩慢，但最後能取得更好的 performance。

Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

在 10 個比較難的遊戲當中測試的結果

尤其在 Solaris 這一款遊戲，可以看到比較明顯的結果。

Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

Adaptive Exploration

最後是針對 Meta-Controller 的實驗。作者將 R2D2+sep. network 以及 NGU+sep. network 拿來比較加上 Meta-Conroller 以及沒有的狀況。

在 10 個比較困難的遊戲當中，可以發現到加上 Meta-Controller(圖片中以 bandit 表示)後可以得到更好的成效。

Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

此外，從上面的圖片中也可以觀察到這樣的 improvement 在 NGU 當中是小許多的。可以認為 separate networks 跟 meta-controller 之間有一些重疊的 benifit

另一方面，有了 meta-controller 之後，即便 discount factor $\gamma$ 異常地大(如 $\gamma = 0.9999$)，模型還是能夠順利學習。在下表當中可以看到 high gamma 的 R2D2，在搭配了 meta-controller 之後得到的成效在 10 款比較困難的遊戲當中有些甚至是能夠比 Average Human 還要強。

Games	R2D2(Retrace) high gamma	Average Human
beam rider	349971.96 $\pm$ 5595.38	16926.50
freeway	32.84 $\pm$ 0.06	29.60
montezuma revenge	1664.89 $\pm$ 1177.26	4753.30
pitfall	0.00 $\pm$ 0.00	6463.70
pong	21.00 $\pm$ 0.00	14.60
private eye	22480.31 $\pm$ 10362.99	69571.30
skiing	-4596.26 $\pm$ 601.04	-4336.90
solaris	14814.76 $\pm$ 11361.16	12326.70
surround	10.00 $\pm$ 0.00	6.50
venture	1774.89 $\pm$ 83.79	1187.50

因此作者認為 meta-controller 提供了更大的普遍性，即便在參數比較異常的狀況下仍然能有很不錯的學習成果。

最後，作者也觀察了在幾款遊戲訓練過程中當中 Meta-Controller 在每個 bandit 選擇中最大的 return 分別落在哪個 bandit，可以發現到不同的遊戲會有不同的偏好。從這裡也可以了解到實際上讓每個 actor 自己調整 policy、適應不同的環境，實際上是有幫助的。

Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

Summary

最後比較 R2D2、NGU、Agent57、MuZero 在所有 Atari games 的優劣，可以發現到 MuZero 雖然在 uncapped mean 有最好的結果，但是在 capped mean 卻是最差的。顯示了 MuZero 在限定幾款遊戲有特別出色的成效，但並不 general。

同時也可以看到 Agent57 有最大的 Capped Mean $100$，亦即 Agent57 能夠在所有的 Atari games 當中獲得比人類平均還要好的成果，除了展現驚人的成果以外，也說明了 Agent57 的普遍性。

同時也能在 R2D2 與 R2D2 bandit 的比較當中明顯看到在所有的成績都有所提升，再次說明了 Meta-Controller 帶來的效益。

Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

最後，Agent57 透過 separate networks、Meta-Controller、long trace 解決了 NGU 的四個缺陷，最終在所有的 Atari games 當中都獲得了超過人類的成效。

Image from Adrià Puigdomènech Badia, Bilal Piot, Steven Kapturowski et al. (2020)

Discussion

Contribution

1. 提出透過 separate networks 解決訓練不穩定、難以收斂的問題
2. 提出 Meta-Controller 來讓每個 actor 自適應不同環境，使模型具有更好的普遍性，並且不同 policy 得以有不同程度的影響
3. 第一個能夠在所有 Atari games 都獲得比 Average Human 更好的成效

值得一看的文章們

• Agent57: Outperforming the human Atari benchmark
• Recurrent Neural Networks in Reinforcement Learning
• MAB - UCB <> TS 基本概念
• Safe and efficient off-policy reinforcement learning.
• Never Give Up: Learning Directed Exploration Strategies
• Adapting Behaviour for Learning Progress
• Agent57
• Distributed Prioritized Experience Replay
• Recurrent experience replay in distributed reinforcement learning